If we divide one whole unit into several equal portions, then one or more of these equal portions can be represented by a fraction.
A fraction is composed of the following three parts:
For example, [latex]\displaystyle>[/latex] is a fraction.
The numerator ‘3’ indicates that the fraction represents 3 equal parts of a whole unit, and the denominator ‘8’ indicates that the whole unit is divided into 8 equal parts, as shown above. The fraction bar indicates that the numerator ‘3’ is divided by the denominator ‘8’.
[latex]\displaystyle>[/latex] is read as “three divided by eight”, “three-eighths”, or “three over eight”. All of these indicate that 3 is the numerator, 8 is the denominator, and the fraction represents 3 of 8 pieces of the whole. The numerator and denominator are referred to as the terms of the fraction.
Note: The denominator of a fraction cannot be zero since a number cannot be divided into zero equal parts.
Any number that can be represented as a fraction is known as a rational number.
Fractions can be represented on a number line. They are plotted in-between whole numbers.
For example, [latex]\displaystyle>[/latex] is represented on a number line as:
When one unit is divided into two equal portions, each portion represents one-half of that unit. One of such equal portions is written as [latex]\displaystyle>[/latex].
Represent the following fractions on a number line:
When one unit is divided into three equal portions, each portion represents one-third of that unit. Two of such equal portions is two-thirds and is written as [latex]\displaystyle>[/latex].
When one unit is divided into five equal portions, each portion represents one-fifth of that unit. Three of such equal portions is three-fifths and is written as [latex]\displaystyle>[/latex].
A proper fraction is a fraction in which the numerator is less than the denominator.
[latex]\displaystyle>[/latex] is a proper fraction because the numerator, 3, is less than the denominator, 8.
An improper fraction is a fraction in which the numerator is greater than or equal to the denominator; i.e., the value of the entire fraction is more than 1.
[latex]\displaystyle>[/latex] is an improper fraction because the numerator 7 is greater than the denominator 4
(i.e., 7 > 4, or [latex]\displaystyle>[/latex] > 1).
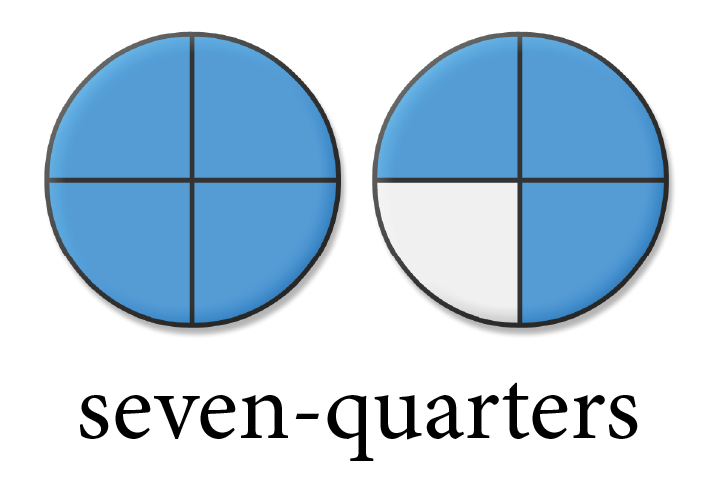
A mixed number consists of both a whole number and a proper fraction, written side-by-side, which implies that the whole number and the proper fraction are added.
[latex]3>[/latex] is a mixed number, where 3 is the whole number, and [latex]\displaystyle>[/latex] is the proper fraction.
[latex]3>[/latex] implies 3 + [latex]\displaystyle>[/latex]
Follow these steps to convert a mixed number to an improper fraction:
Step 1: Multiply the whole number by the fraction’s denominator and add this value to the fraction’s numerator.
Step 2: The resulting answer will be the numerator of the improper fraction.
Step 3: The denominator of the improper fraction is the same as the denominator of the original fraction in the mixed number.
Example: Convert [latex]3>[/latex] to an improper fraction.
Step 2: 24 + 5 = 29. The numerator will be 29.
Step 3: The denominator will be 8.
Therefore, [latex]3>[/latex] = [latex]\displaystyle>[/latex]
Note: You can perform the above steps in a single line of arithmetic as follows:
Four circles are divided into 8 equal pieces. Three of the four circles are completely shaded, and five pieces of the last circle are shaded for 29 pieces.
Follow these steps to convert an improper fraction to a mixed number:
Step 1: Divide the numerator by the denominator.
Step 2: The quotient becomes the whole number, and the remainder becomes the numerator of the fraction portion of the mixed number.
Step 3: The denominator of the fraction portion of the mixed number is the same as the denominator of the original improper fraction.
Example: Convert [latex]\displaystyle>[/latex] to an improper fraction.
Step 1: Divide 29 by 8.
Step 2: The quotient (3) becomes the whole number, and the remainder (5) becomes the numerator of the fraction portion of the mixed number.
Step 3: The denominator of the fraction portion of the mixed number (8) is the same as the denominator of the original improper fraction (8).
Therefore, [latex]\displaystyle>[/latex] = [latex]3>[/latex]
When a fraction’s numerator and denominator are either multiplied by the same number or divided by the same number, the result is a new fraction known as an equivalent fraction. Equivalent fractions have the same value.
That is, the same part (or portion) of a whole unit can be represented by different fractions.
[latex]\displaystyle>[/latex], [latex]\displaystyle<\frac>[/latex], [latex]\displaystyle>[/latex], [latex]\displaystyle<\frac>[/latex], [latex]\displaystyle>[/latex], … are equivalent fractions.
Find two equivalent fractions of [latex]\displaystyle>[/latex] by raising to higher terms.
To find an equivalent fraction of [latex]\displaystyle>[/latex], multiply both the numerator and denominator by 2. The resulting equivalent fraction is [latex]\displaystyle>[/latex].
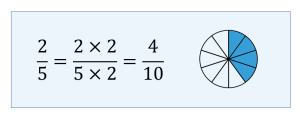
To find an equivalent fraction of [latex]\displaystyle>[/latex], multiply both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle>[/latex].
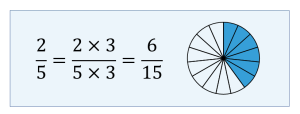
Therefore, [latex]\displaystyle>[/latex] and [latex]\displaystyle>[/latex] are equivalent fractions of [latex]\displaystyle>[/latex].
Find two equivalent fractions of [latex]\displaystyle>[/latex] by reducing to lower terms.
To find an equivalent fraction of [latex]\displaystyle>[/latex], divide both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle>[/latex].
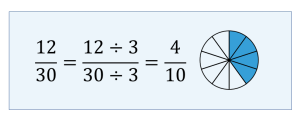10 is found by dividing the top and bottom by 3. The resulting fraction is 4/10. The pie chart shows 4 of the 10 slices shaded." width="352" height="135" />
To find another equivalent fraction, divide the numerator and denominator by 2. The resulting equivalent fraction is [latex]\displaystyle>[/latex].
Or, the lowest terms can be found by dividing both the numerator and denominator of the original fraction, [latex]\displaystyle>[/latex], by 6.
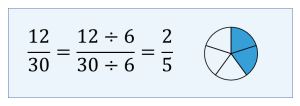
Therefore, [latex]\displaystyle>[/latex] and [latex]\displaystyle>[/latex] are equivalent fractions of [latex]\displaystyle>[/latex].
Note: The fraction [latex]\displaystyle>[/latex] cannot be further reduced, as 2 and 5 do not have any common factors.
Therefore, [latex]\displaystyle>[/latex] is a fraction in its lowest (or simplest) terms. We will learn more about this further in the section.
If the cross products of two fractions are equal, then the two fractions are equivalent fractions, and vice versa (i.e., if the fractions are equivalent, then their cross products are equal).
a × d and b × c are known as cross products
For example, [latex]\displaystyle>[/latex] and [latex]\displaystyle>[/latex] are equivalent fractions because their cross products, 3 × 20 and 5 × 12, are equal:
Classify the pair of fractions as ‘equivalent’ or ‘not equivalent’ by using their cross products.
